Interest Rate Brain Teasers
Want to test your knowledge of interest rate concepts? You've come to the right place! These questions are the ones we use when sending new team members through LoanBoss Bootcamp, and they can be a bit tricky (on purpose).
And you'll be needing these:
Caveat: we used back of the envelope math for these brain teaser purposes — this is mainly about catching the tricks in the question. So, for example, we'll overlook a 30 year amort when considering what the average remaining loan balance is, since that is not going to bleed off enough principal to have a huge effect on the math — if it's a 30 or 25 year amort, the real answer will just be slightly less than back of the envelope math, but it'll be pretty dang close!
Okay, let's do it.
A borrower closed on a $27.22mm 10-year interest only, LIBOR + 2.05% loan on 3/1/16, with a 0.25% floor that they did not buy out. They then locked a swap for an all-in fixed rate of 3.56%, with a 0.25% credit charge.
- On the day they locked the swap, what did the market think LIBOR was going to average over the life of the loan?
It's the same formula as above, but backing into the index component. All-in rate of 3.56% - 2.05% spread - 0.25% credit charge = 1.26%. The 1.26% is mid on the day of close, and the number the swap provider saw the market predicting LIBOR to average over the next 10 years.
- How much revenue did the bank make on this swap?
You need 2 things for this: the given credit charge of 0.25%, and the PV01.
Present Value of 1bp is calculated back of the envelope with: the loan amount x years remaining x 0.01%. The PV01 of this loan on day of close = $27.22mm x 10 years x 0.01% = $27,220 (aka the dollar value of a single basis point).
But the credit charge is for twenty five basis points, so $27,220 x 25bps = $680,500. This is the bank's profit on the swap.
What's the penalty on a fully amortizing $27.1mm internally fixed loan with a 10 year term, closed on 3/1/16 at 10T + 2.00% for an all-in rate of 4.00%?
To solve for a prepayment penalty, you need the DV01 (which is really the same concept as PV01, except different terminology for non-swaps) x the rate differential. The full equation is: (average remaining loan balance x years remaining x 0.01%) x (current rate in bps - replacement rate in bps), and that will get you a pretty close number.
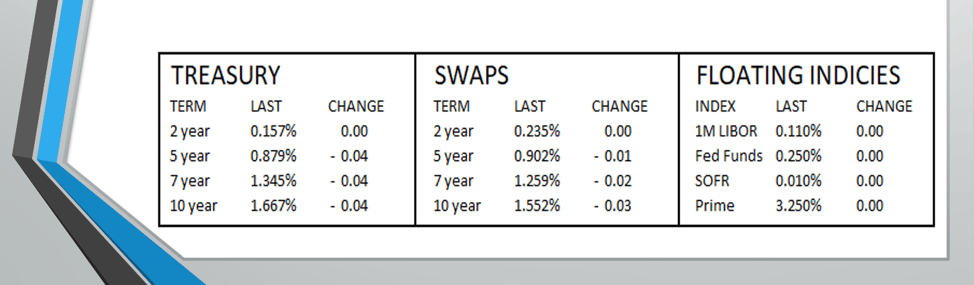
For reference, "replacement rate" is the rate the lender could redeploy those funds at for the remainder of the term, if the borrower paid off today. And for this problem, we'll look at the Treasury rates at the top of the page.
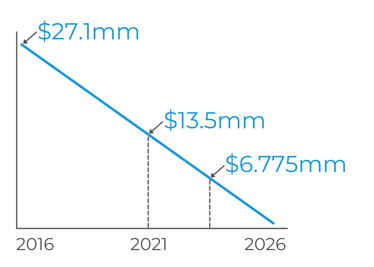
DV01 = $27.1mm x 5 years x 0.01%? Nope. Average remaining loan balance. This loan closed in 2016, so it's halfway to maturity. Why does that matter? It's fully amortizing, so the balance in 2026 will be $0. At the halfway mark, you're already at a $13.55mm balance.
But we're not done there either. We still need the average remaining balance. If we have $13.55mm today, and we'll hit $0 at the maturity date, the average remaining today acts more like $13.55mm / 2 = $6.775mm.
So, the DV01 = $6.775mm x 5 years x 0.01% = $3,387.5
Last component: rate differential. The current rate is 4.00%, but what could the lender redeploy these funds at for the remainder of the term? With 5 years remaining, the replacement rate would be 87.9 bps (the 5 year Treasury). If their fixed rate is 4.00%, then 4.00% - 0.879% = 3.121%.
The penalty today = $3,387.5 x 312.1 bps = $1.05mm.
All else being equal, which will have a higher prepayment penalty — a swap or a CMBS deal?
The CMBS deal will always have the higher prepay, all else equal, because it is against you on day 1. Comparatively, on the day you lock a swap, aside from the credit charge, you've locked at mid - if rates move exactly as expected, you'll break even.
The same does not hold true for the CMBS, which is immediately against you by the spread.
To learn more about CMBS loans, download our eBook or read the blog!
If rates move exactly as expected over the next five years, how much should the swap breakage cost be in 3 years on a $25mm 5 year swap, assuming the bank made no profit?
Assuming no credit charge, the breakage cost will be $0.
Why? When this borrower locked their swap, they locked at a mid rate, aka what markets thought rates would average over the next 5 years.
The typical breakage cost comes from markets over-estimating the path of rates, but no overestimation = no breakage.
A borrower's closing yesterday got pushed to today. They are closing on a $46mm 10 year I/O at swaps + 2.00% (assume they lock at mid).
- How much interest will they have saved over the life of the loan by locking today instead of yesterday?
At the very top of the page, we can start by pulling the change in 10 year swap rate, which is a 3 bps decrease from the day before. The fact there was a 3 bps decrease is all we need to know from there.
Next step is to find the DV01, or the value of each 1 basis point, which we can just multiply by 3. DV01 = $46mm x 10 x 0.01% = $46,000.
So that 0.03% decrease from yesterday, times the value of a single basis point, and this borrower saved approximately $138,000 by locking a day later.
- All else being equal, how much lower will their penalty be in five years because they locked today instead of yesterday?
You could pull out the full equation here, and... heck, we will do it just for fun:
Scenario 1: the borrower locked yesterday at 1.582%. Plus the 2.00% spread, their all-in rate is 3.582%.
Scenario 2: the borrower locked today at 1.552%. Plus the 2.00% spread, their all-in rate is 3.552%.
In both cases, the replacement rate in 5 years will be the 5 year swap rate, at a current (in this blog) 90.2 basis points.
And that DV01 we can cut in half to $23,000 (since the time remaining cut in half) - so now for the rate differentials:
Scenario 1: 358.2 bps - 90.2 bps = 268 bps x $23,000 = a projected $6.164mm prepayment
Scenario 2: 355.2 bps - 90.2 bps = 265 bps x $23,000 = a projected $6.095mm prepayment
Because the borrower locked a day later, their prepayment is $69,000 less than it would have been. The difference in the prepayment come 5 years into the term will be about $69,000 (nice).
But we also appreciate shortcuts...
At 5 years left, the DV01 is $23,000. The difference will be 3 basis points, so: $23,000 x 3 = $69,000.
Boom.
A borrower has a $2mm swap MtM and wants to refi when the MtM gets to $1.5mm. The swap has 7 years remaining with an interest only notional of $40mm. They ask you how much rates need to move and in which direction. What do you tell them?
Could have floated instead! 😜
Just kidding - first step: PV01. $40mm x 7 years x 0.01% = $28,000.
Next step: what does the MtM need to decrease by? $2mm - $1.5mm = $500,000. So $500k is the decrease in breakage that triggers a refi scenario for this borrower.
Then, we can back into the basis point change with the formula of the PV01 x basis point change = dollar amount change. So $28,000 x basis point change = $500,000. Then that basis point change must be 18 basis points.
To take an extra step, we'll add that rates would need to rise by 18 bps to hit the $1.5mm MtM. Why? Just to take a look mathematically, back to the rate differential piece of the full equation: the higher the replacement rate, the lower the rate differential is being multiplied by.
Example: given a PV01 of $10,000 and current rate of 2.00%...
- Replacement rate of 90bps -> $10,000 x (200 - 90) = $1.1mm
- Replacement rate of 100 bps -> $10,000 x (200 - 100) = $1.0mm
On 4/6/19, a borrower closed on a 3+1+1 $17.77mm interest only loan on LIBOR + 2.00% with a floor set at the 3 year swap rate of 0.80%. Over the first year after close, LIBOR averaged 0.67%. During the second year, LIBOR averaged 0.13%. How much has the floor cost them in the first two years?
Year 1: LIBOR is at 0.67%, below the 0.80% floor by 13 basis points. So for the first year, this borrower paid that extra 13 bps in interest because of the floor.
Year 2: LIBOR is at 0.13%, below the 0.80% floor by 67 basis points. So for the second year, this borrower paid that extra 67 bps in interest because of the floor.
In total: over the first two years, the floor has cost this borrower 80 bps in extra interest, or $142,160.
Want to try some more? Download more problems here and give them a shot!
Or give your brain a break with some CRE fun! Check out these Buzzwords or Fun Facts!
